La detección de anomalías es una de las tareas más importantes en la industria, especialmente cuando se trata de monitorizar maquinaria crítica como compresores de aire. En este artículo te explico, de manera sencilla, qué es la distancia de Mahalanobis, por qué es tan potente para detectar anomalías y cómo la hemos aplicado en un caso real usando autoencoders.
¿Qué es la distancia de Mahalanobis?
Imagina que tienes un conjunto de datos con varias variables (temperatura, presión, vibración, etc.). Cuando quieres saber si una nueva observación es “normal” o “extraña”, lo más sencillo es calcular la distancia a la media de los datos normales. Pero, ¿qué pasa si tus variables están correlacionadas o tienen escalas muy diferentes? Aquí es donde la distancia de Mahalanobis brilla.
La distancia de Mahalanobis es una medida que tiene en cuenta no solo la media de los datos, sino también cómo se relacionan entre sí las variables (su covarianza). Es decir, no trata igual una desviación en una variable que suele variar mucho, que en otra que casi nunca cambia. Además, si dos variables suelen moverse juntas, la distancia de Mahalanobis lo tiene en cuenta y no penaliza tanto esas combinaciones.
Fórmula sencilla:
La distancia de Mahalanobis entre un punto ( x ) y la media ( μ ) de los datos normales es:
d = √[(x – μ)ᵀ Σ⁻¹ (x – μ)]
donde ( Σ⁻¹ ) es la matriz de covarianza de los datos normales.
¿Por qué es mejor que la distancia euclídea o el MSE?
- Ajusta automáticamente la importancia de cada variable según su variabilidad.
- Tiene en cuenta las correlaciones entre variables.
- Es independiente de la escala de las variables.
¿Cómo la usamos en la detección de anomalías?
En nuestro notebook, aplicamos la distancia de Mahalanobis para mejorar la detección de anomalías en los datos de sensores de un compresor de aire. El flujo fue el siguiente:
- Entrenamos un autoencoder: Este modelo aprende a reconstruir los datos normales. Si un dato es “raro”, el autoencoder lo reconstruye mal.
- Calculamos los residuos: Para cada muestra, restamos la reconstrucción del dato original.
- Calculamos la matriz de covarianza de los residuos: Así entendemos cómo suelen variar los errores de reconstrucción en condiciones normales.
- Calculamos la distancia de Mahalanobis: Para cada muestra, medimos qué tan “extraño” es su patrón de error de reconstrucción, teniendo en cuenta la covarianza.
- Definimos un umbral: Si la distancia de Mahalanobis es muy alta (por ejemplo, mayor que el percentil 95 de las distancias en los datos normales), consideramos que es una anomalía.
¿Qué ganamos con esto?
- Menos falsos positivos: No saltan alarmas por pequeñas desviaciones en variables que suelen variar mucho.
- Más sensibilidad a anomalías reales: Detecta patrones de fallo sutiles que el MSE o la distancia euclídea podrían pasar por alto.
- Mejor interpretación: Puedes visualizar la distribución de distancias y entender mejor qué es “normal” y qué no.
Ejemplo concreto del notebook
En el notebook, después de entrenar el autoencoder, calculamos la distancia de Mahalanobis para cada muestra de test. Así, logramos distinguir mucho mejor entre el funcionamiento normal y los diferentes tipos de fallo del compresor. El resultado: una detección de anomalías más robusta y fiable, ideal para aplicaciones industriales donde los errores pueden ser costosos.
La matriz de confusión empleando el error cuadrático medio (MSE) expresa una clara deficiencia del modelo para detectar correctamente las anomalías.
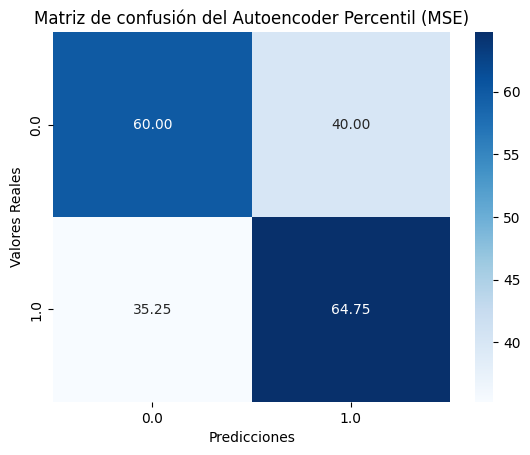
En cambio, al emplear la distancia Malahanobis y considerar la correlación entre las distintas variables predictoras, el rendimiento aumenta notablemente:

Conclusión
La distancia de Mahalanobis es una herramienta sencilla pero muy poderosa para la detección de anomalías, especialmente cuando tus datos tienen muchas variables correlacionadas. Si trabajas con sensores industriales, datos financieros o cualquier sistema complejo, te recomiendo probarla: puede marcar la diferencia entre detectar un fallo a tiempo o no.
