Gaussian Mixture Models (GMM) aplicados a mantenimiento predictivo: fundamentos, implementación y resultados en una bomba de agua

1) Fundamentos: ¿qué es un GMM y por qué resulta adecuado para detectar anomalías?

Un Gaussian Mixture Model (GMM) modela la distribución de los datos como una mezcla de gaussianas. En lugar de suponer una única distribución normal, el GMM reconoce la posible existencia de subpoblaciones (componentes) con medias y covarianzas distintas, algo habitual cuando un activo opera en regímenes o condiciones de trabajo diferentes.

Idea esencial

El modelo asigna pesos a cada componente (proporciones de mezcla).
Cada componente es una normal multivariante con su media y matriz de covarianzas.
La probabilidad de un dato es la suma ponderada de las probabilidades de cada componente.

Ventaja para la detección de anomalías
Si se entrena el GMM exclusivamente con datos en condición sana, el modelo aprende la región del espacio de variables que resulta plausible para la operación normal. En inferencia, se evalúa la log-verosimilitud de nuevas observaciones; valores bajos respecto a lo observado en entrenamiento indican anomalía. Es un enfoque no supervisado (one-class-like) especialmente útil cuando los fallos son escasos o heterogéneos.

Entrenamiento con EM (esquema resumido)

E-step: se calculan las responsabilidades de cada componente sobre cada muestra con los parámetros actuales.
M-step: se actualizan pesos, medias y covarianzas según dichas responsabilidades.
Se itera hasta la convergencia. En la práctica, se emplea sklearn.mixture.GaussianMixture.

Decisiones de modelado relevantes

Número de componentes (K): iniciar con 2–5 y contrastar con BIC/AIC y criterio de dominio.
Tipo de covarianza (spherical, diag, tied, full):
- full captura correlaciones realistas entre variables (más parámetros).
- diag es más ligera cuando hay muchas variables y datos limitados.
Regularización (reg_covar) para evitar problemas numéricos.
Inicialización: k-means suele ser estable; conviene probar varias semillas.

GMM frente a alternativas (síntesis)

K-Means: no modela densidad; menos adecuado para rarezas.
One-Class SVM: potente, pero más sensible a hiperparámetros.
Autoencoders: muy expresivos, requieren más datos y cómputo, menos transparentes.
HMM: preferible si la dinámica temporal (transiciones entre estados) es determinante; si basta con un análisis estadístico por ventana, GMM es una opción sólida.

2) Implementación: caso práctico en una bomba de agua

2.1. Datos y variables (features)

Se trabaja con series temporales de sensores de una bomba de agua (p. ej., presión, caudal, vibración, temperatura). El objetivo es modelar la operación sana y después puntuar nuevas observaciones.

Preprocesado aplicado (enfoque típico)

Limpieza y selección: tratamiento de ausentes y eliminación de valores atípicos extremos; selección de variables relevantes.
Segmentación en ventanas: cálculo de agregados por ventana (media, desviación típica, picos, curtosis, energía en bandas, etc.). Aporta contexto temporal de corto plazo.
Estandarización: ajuste de StandardScaler/MinMaxScaler solo con datos sanos y aplicación posterior al resto.
Partición: conjunto de entrenamiento sano para ajustar el GMM y conjunto de prueba con sano/fallo para evaluar.

2.2. Entrenamiento del GMM

Configuración de partida robusta en operación multirégimen:

from sklearn.mixture import GaussianMixture

gmm = GaussianMixture(
    n_components=3,          # ajustar con BIC/AIC o criterio de dominio (p. ej., 2–5)
    covariance_type='spherical',
    reg_covar=1e-6,          # regularización numérica
    init_params='kmeans',    # inicialización estable
    max_iter=500,
    random_state=42
)
gmm.fit(X_train_healthy)

2.3. Puntuación y umbral

La puntuación base es la log-verosimilitud por muestra:

import numpy as np

logp_train = gmm.score_samples(X_train_healthy)  # densidad en log
logp_test  = gmm.score_samples(X_test)           # mezcla sano/fallo

Para el umbral, un criterio claro y justificable es el cuantil sobre el conjunto sano:

tau = np.quantile(logp_train, 0.01)    # 1% inferior; ajustar según tolerancia al riesgo
y_pred = (logp_test < tau).astype(int) # 1 = anomalía

Puede optimizarse tau en validación para F1 o, más orientado a mantenimiento, sensibilidad (recall) a FPR fijada, dado el coste de no detectar un fallo.

2.4. Métricas e inspección cualitativa

Matriz de confusión: TP/FP/FN/TN (se insertará como figura).
Precisión / Sensibilidad / F1: ajuste del compromiso según costes.
ROC/PR: si se dispone de puntuación continua.
Evolución temporal de la log-verosimilitud: descensos sostenidos suelen anticipar degradación.
Interpretabilidad operativa: análisis de z-scores por variable en ventanas anómalas para identificar sensores que explican la rareza.

3) Resultados e interpretación

Figura 1 — Matriz de confusión del GMM

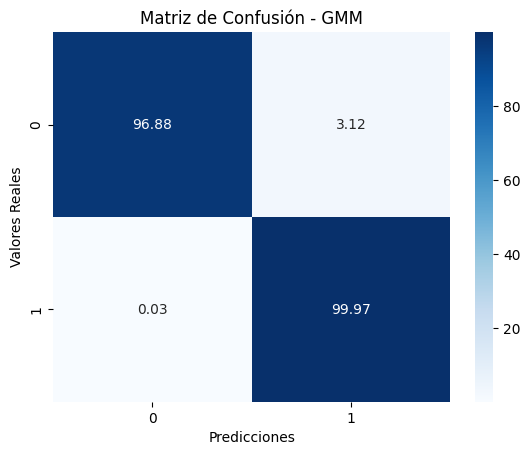
3.1. Lectura de la matriz

TP elevados: el GMM separa adecuadamente patrones no plausibles frente a lo sano.
FP: suelen concentrarse en cambios de régimen o deriva (p. ej., variaciones ambientales). Posibles actuaciones:
- aumentar K o emplear full si no se estaba usando;
- segmentar por régimen operativo;
- recalibrar el umbral fijando una FPR asumible.
FN: fallos cercanos a la normalidad (degradación sutil o gradual). Mejoras:
- enriquecer variables (espectro de vibración, estadísticas móviles, tendencias);
- reducir el umbral (estrategia orientada a sensibilidad);
- incorporar estructura temporal (suavizado del score o transición a HMM).

3.2. Gráficas recomendadas

Distribución de log-verosimilitud en sano vs fallo (grado de separación).
Serie temporal de log-verosimilitud con el umbral y los disparos de alerta.
Ablación de hiperparámetros: impacto de K, covariance_type y del umbral.

3.3. Conclusiones prácticas del caso

El GMM capta multi-régimen de forma eficaz; full + K>1 reduce falsos positivos cuando hay variabilidad real.
Un umbral cuantílico es trazable y defendible ante operación/mantenimiento.
El preprocesado y la calidad de las variables son determinantes para la estabilidad del modelo.

4) Guía reproducible (del cuaderno a producción)

Datos y esquema: fijar variables y escalado (ajuste del scaler exclusivamente con datos sanos).
Selección de K: punto de partida con BIC (2–5) y validación con criterio de negocio.
Entrenamiento: GaussianMixture(..., covariance_type='spherical', reg_covar=1e-6, max_iter≥300).
Umbral: cuantil sobre score_samples en sano o ajuste dirigido a sensibilidad objetivo.
Supervisión: control de deriva en puntuación y variables; política de reentrenos.
Explicabilidad: z-scores por sensor en ventanas disparadas.
Alarmado robusto: suavizado temporal (p. ej., activar alerta si 3 de las 5 últimas ventanas están por debajo del umbral).

5) Fragmento mínimo (scikit-learn)

import numpy as np
from sklearn.preprocessing import StandardScaler
from sklearn.mixture import GaussianMixture
from sklearn.metrics import classification_report, roc_auc_score

# 1) Escalado ajustado SOLO con sano
scaler = StandardScaler().fit(X_train_healthy)
Xtr = scaler.transform(X_train_healthy)
Xte = scaler.transform(X_test)

# 2) Entrenamiento del GMM
gmm = GaussianMixture(
    n_components=3, covariance_type='full',
    reg_covar=1e-6, init_params='kmeans',
    max_iter=500, random_state=42
).fit(Xtr)

# 3) Puntuación y umbral
logp_tr = gmm.score_samples(Xtr)
logp_te = gmm.score_samples(Xte)
tau = np.quantile(logp_tr, 0.01)          # ajustar según tolerancia al riesgo
y_pred = (logp_te < tau).astype(int)      # 1 = anomalía

# 4) Métricas
print(classification_report(y_test, y_pred, digits=3))
try:
    auc = roc_auc_score(y_test, -logp_te)  # mayor valor => más anómalo
    print(f"ROC-AUC: {auc:.3f}")
except Exception:
    pass

6) Limitaciones y extensiones

Hipótesis gaussiana: colas pesadas o multimodalidad compleja pueden requerir mixturas no gaussianas u otros modelos de densidad.
Temporalidad: si la dinámica es clave, considerar HMM o, al menos, suavizado temporal de la puntuación.
Deriva: cambios de entorno pueden desplazar la distribución; definir recalibración y reentrenos.
Coste de falsos positivos: si la inspección es costosa, trabajar a FPR fijada y establecer una verificación de segunda fase.

7) Conclusión

Los GMM constituyen una alternativa sencilla, interpretable y eficaz para la detección de anomalías cuando predomina el registro sano y los fallos son escasos. En el caso de la bomba de agua, la combinación de variables físicas + GMM entrenado en sano + umbral cuantílico permite obtener un detector que anticipa degradaciones y facilita la toma de decisiones de mantenimiento.

AUDITAI

IA3migdem