En el campo del mantenimiento predictivo, la predicción del Time to Failure (TTF) es una de las técnicas más valiosas para optimizar los programas de mantenimiento y reducir los tiempos de inactividad no planificados. A diferencia de los enfoques tradicionales basados en intervalos fijos, la predicción del TTF utiliza datos en tiempo real y técnicas avanzadas de análisis para estimar cuándo ocurrirá el próximo fallo en un componente o sistema. Esta capacidad de predicción permite a las organizaciones planificar actividades de mantenimiento justo cuando son necesarias, evitando tanto el mantenimiento excesivo como los fallos inesperados.
¿Qué es el Time to Failure y cómo se relaciona con el RUL?
El Time to Failure (TTF) o tiempo hasta el fallo es una medida que indica el tiempo esperado antes de que un componente o sistema experimente un fallo. Este concepto está estrechamente relacionado con el Remaining Useful Life (RUL) o vida útil restante, pero con algunas diferencias sutiles.
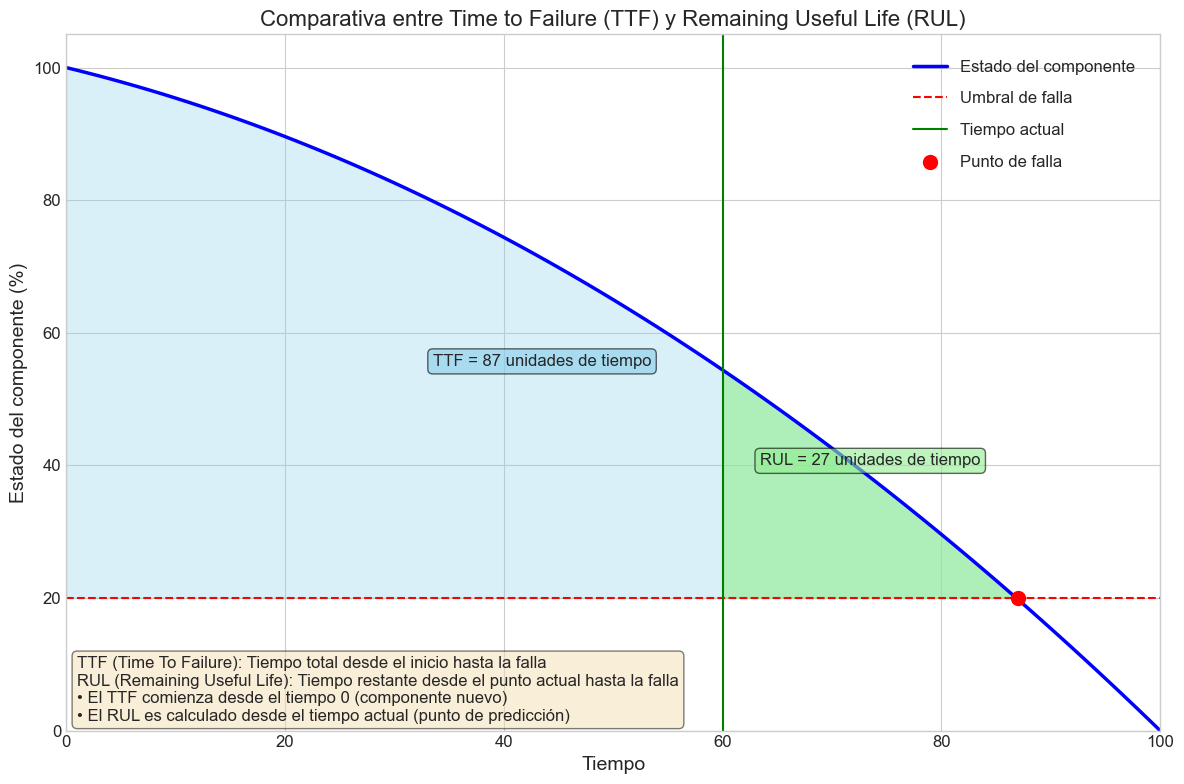
Diferencias entre TTF y RUL
- Perspectiva: El TTF se enfoca en predecir el momento específico del fallo, mientras que el RUL se centra en la cantidad de vida útil que queda.
- Unidades de medida: El TTF generalmente se expresa en unidades absolutas de tiempo (horas, días), mientras que el RUL puede expresarse tanto en tiempo como en ciclos de operación o unidades de trabajo.
- Aplicación en decisiones: El TTF se utiliza principalmente para programar mantenimiento, mientras que el RUL se emplea para evaluar el valor residual y planificar reemplazos.
Aunque conceptualmente diferentes, tanto el TTF como el RUL son fundamentales en el mantenimiento predictivo. Mientras el RUL nos proporciona una visión de la degradación gradual, el TTF nos ayuda a establecer plazos concretos para la intervención.
Métodos para la predicción del Time to Failure
La predicción del TTF ha evolucionado significativamente con el avance de las técnicas de análisis de datos y aprendizaje automático. Actualmente, existen diversos enfoques que podemos clasificar en tres grandes categorías:
1. Métodos basados en física
Estos modelos se fundamentan en ecuaciones físicas que describen los mecanismos de degradación de los componentes. Utilizan principios de mecánica, termodinámica, electromagnetismo y otras disciplinas para modelar cómo evolucionan los fallos a lo largo del tiempo.
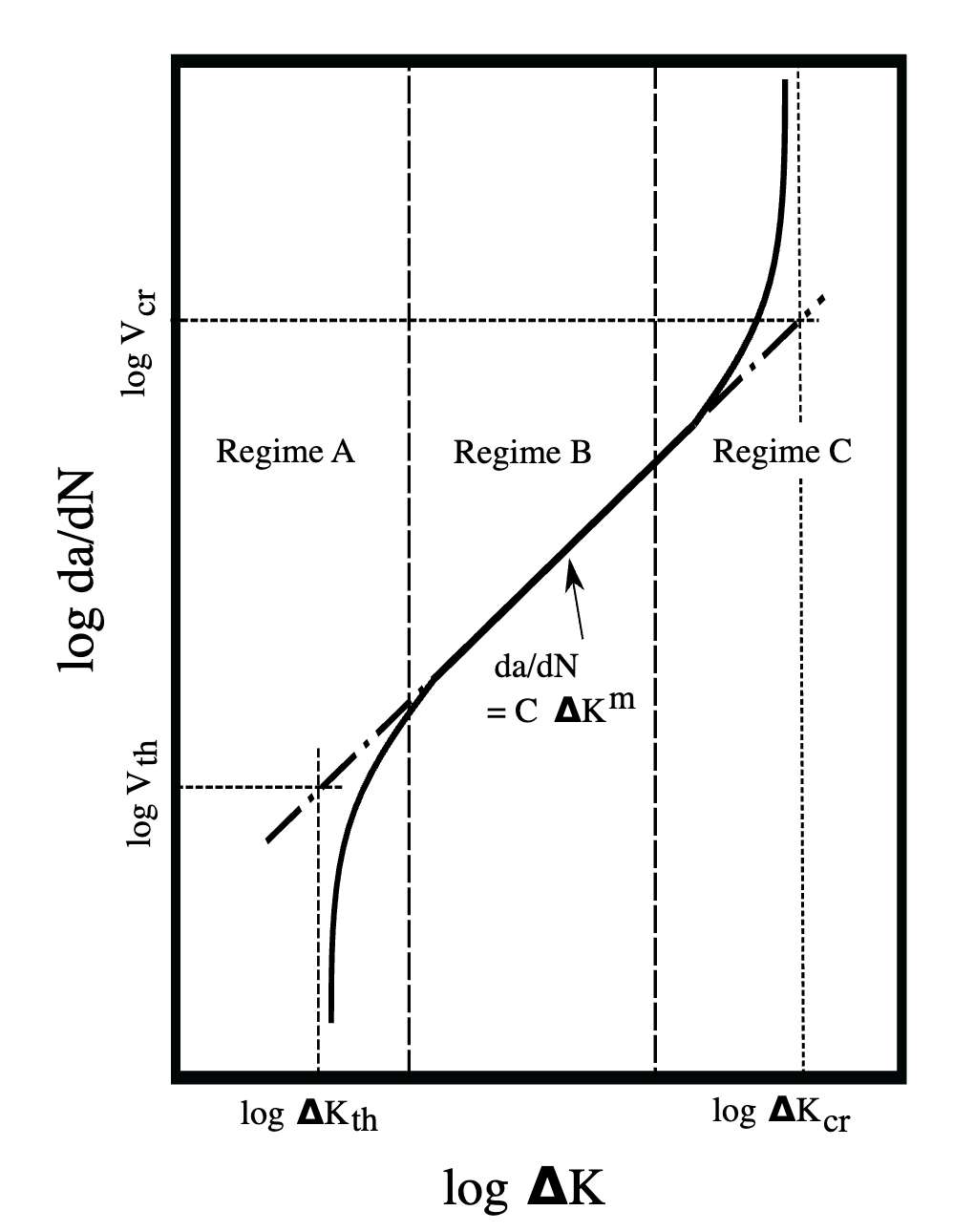
Un ejemplo típico es el modelo de Paris-Erdogan para la propagación de grietas por fatiga, que describe cómo una grieta crece con cada ciclo de carga hasta alcanzar un tamaño crítico que provoca el fallo:
da/dN = C(ΔK)^m
Donde:
- da/dN es la tasa de crecimiento de la grieta por ciclo
- ΔK es el rango del factor de intensidad de tensiones
- C y m son constantes del material
2. Métodos basados en datos
Estos enfoques utilizan datos históricos y técnicas de aprendizaje automático para identificar patrones y tendencias que preceden a los fallos. A diferencia de los métodos físicos, no requieren un conocimiento profundo de los mecanismos de fallo, sino grandes cantidades de datos históricos de calidad.
Entre las técnicas más utilizadas encontramos:
- Redes neuronales: Especialmente efectivas para capturar relaciones no lineales complejas entre las variables de entrada y el TTF.
- Random Forest: Proporciona robustez frente al ruido y buena interpretabilidad, permitiendo identificar las variables más influyentes.
- Modelos de series temporales: Como ARIMA y LSTM, excelentes para capturar patrones temporales en los datos de degradación.
3. Métodos híbridos
Combinan el conocimiento físico con técnicas basadas en datos para aprovechar las ventajas de ambos enfoques. Son particularmente útiles cuando se dispone de modelos físicos parciales o cuando los datos históricos son limitados.
Ventajas de los métodos híbridos
- Mayor precisión: Incorporan conocimiento de dominio junto con patrones identificados en los datos.
- Mejor interpretabilidad: A diferencia de las «cajas negras» del aprendizaje automático puro, permiten entender los factores físicos que influyen en las predicciones.
- Necesitan menos datos: Al incorporar conocimiento físico, requieren menos datos históricos para entrenar modelos precisos.
Aplicación del TTF en la industria
La predicción del Time to Failure está transformando las estrategias de mantenimiento en múltiples sectores industriales. Algunos ejemplos destacados incluyen:
- Aeronáutica: Predicción de fallos en turbinas y componentes críticos de aeronaves, permitiendo optimizar los programas de mantenimiento sin comprometer la seguridad.
- Energía: Monitorización de turbinas eólicas y equipos de generación para predecir fallos y programar mantenimiento durante períodos de baja demanda.
- Manufactura: Estimación del TTF en robots y líneas de producción para minimizar interrupciones no planificadas.
- Transporte: Predicción de fallos en flotas de vehículos, optimizando la disponibilidad y reduciendo costos operativos.
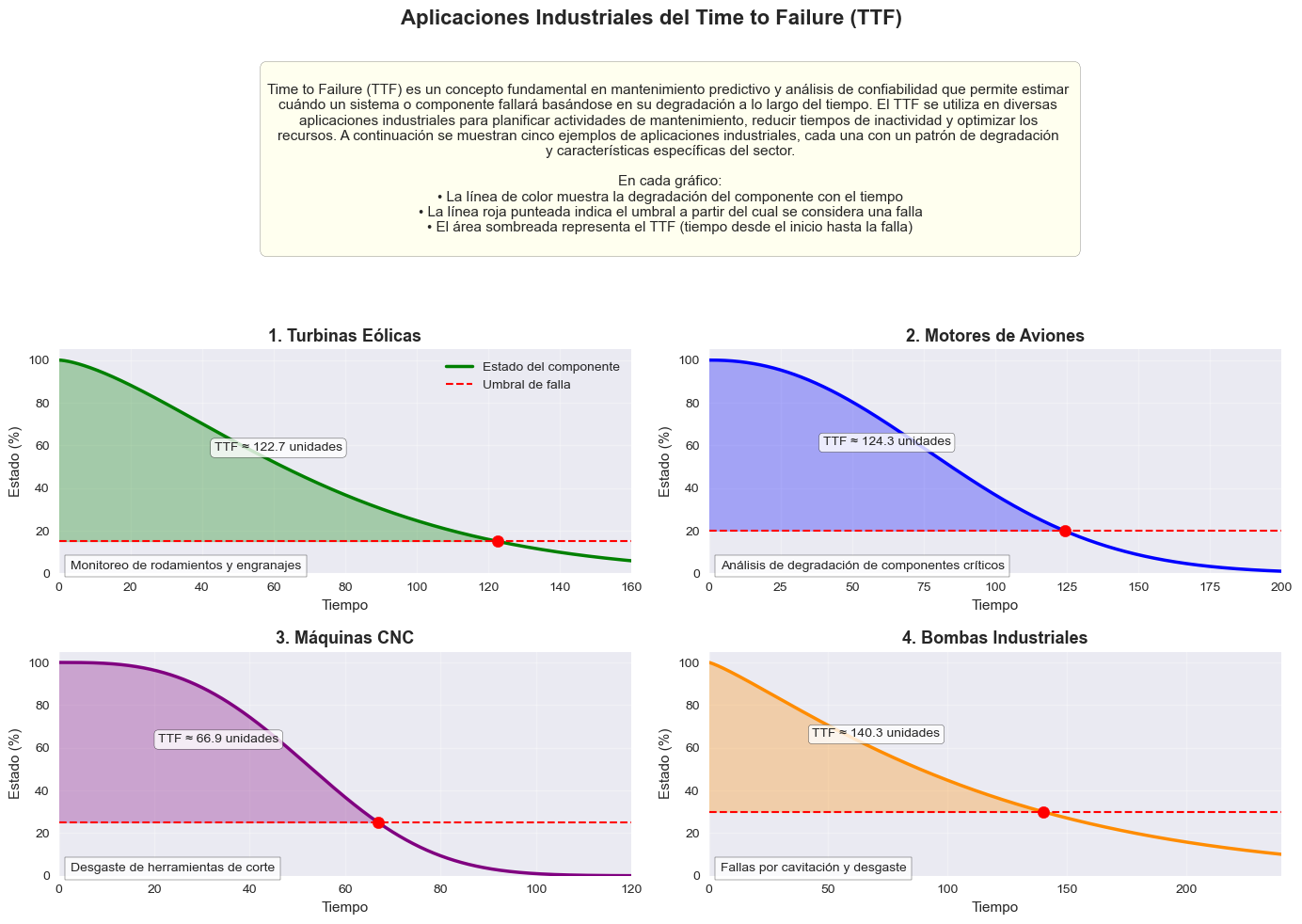
Un caso particularmente interesante es el de la industria ferroviaria, donde la predicción del TTF en componentes como rodamientos, bogies y sistemas de frenado ha permitido reducir significativamente los retrasos por fallos inesperados y optimizar los ciclos de mantenimiento.
Desafíos en la predicción del TTF
A pesar de sus beneficios, la implementación de sistemas eficaces de predicción del TTF presenta varios desafíos:
- Variabilidad operativa: Las condiciones de operación cambiantes pueden afectar significativamente el proceso de degradación.
- Interacciones complejas: Los componentes no se degradan de forma aislada, sino que interactúan entre sí, complicando las predicciones.
- Eventos raros: Algunos fallos ocurren con tan poca frecuencia que es difícil recopilar datos suficientes para modelarlos adecuadamente.
- Incertidumbre: Las predicciones del TTF siempre conllevan incertidumbre, que debe ser cuantificada y gestionada.
Cuantificación de la incertidumbre
Un enfoque cada vez más común para abordar la incertidumbre en las predicciones del TTF es la utilización de distribuciones de probabilidad en lugar de estimaciones puntuales. Esto permite expresar el TTF como una distribución que refleja la confianza en diferentes intervalos de tiempo:
P(Tfallo ≤ t) = F(t) = ∫₀ᵗ f(τ)dτ
Donde:
- F(t) es la función de distribución acumulativa
- f(τ) es la función de densidad de probabilidad del tiempo de fallo
Herramientas y frameworks para la predicción del TTF
Existen diversas herramientas y frameworks que facilitan la implementación de modelos de predicción del TTF:
- Python con scikit-learn, TensorFlow y PyTorch: Para el desarrollo de modelos personalizados de aprendizaje automático.
- R con paquetes como survival y flexsurv: Especialmente útiles para análisis de supervivencia y modelos estadísticos avanzados.
- Plataformas comerciales: Como IBM Maximo, Predikto, Uptake y C3.ai, que ofrecen soluciones integrales para el mantenimiento predictivo.
Estas herramientas permiten desde el procesamiento de datos hasta la visualización y el despliegue de modelos de predicción del TTF en entornos de producción.
Referencias
- Paris, P., & Erdogan, F. (1963). A critical analysis of crack propagation laws. Journal of Basic Engineering, 85(4), 528-534.
- Lei, Y., Li, N., Guo, L., Li, N., Yan, T., & Lin, J. (2018). Machinery health prognostics: A systematic review from data acquisition to RUL prediction. Mechanical Systems and Signal Processing, 104, 799-834.
- Saxena, A., Goebel, K., Simon, D., & Eklund, N. (2008). Damage propagation modeling for aircraft engine run-to-failure simulation. 2008 International Conference on Prognostics and Health Management.
