Los Normalizing Flows son un tipo de Probabilistic Generative Model, esto significa que lo que buscamos simular con el modelo es la distribución de una variable X, usando los datos que tenemos (x_i), describiéndola con una función de densidad p_X(x) y que además es parametrizado por un valor θ.

La idea principal de este modelo es sencilla: queremos encontrar una función f de tal manera que f : X → Z donde Z es el espacio de ruido gaussiano. Con esto, conseguimos que f (x) = z nos de un ruido gaussiano. Esta función ha de ser invertible y diferenciable, lo que permite que luego a raiz de ruido gaussiano aleatorio, podamos implementar la inversa de esta función y generar datos que provienen de la misma distribución que los reales, y por tanto se parezcan a ellos. Podemos usar la función de cambio de variables para escribir la función de densidad p_X(x), en función de nuestra transformación f y nuestro espacio Z como:

p_X (x) = p_Z (f (x))*|det Df (x)|

Tenemos una serie de Requisitos de f que necesitamos que se cumplen para poder calcular p_X de esta manera:

1. Invertible: Existe f⁻¹.
2. Diferenciable: Para poder calcular el jacobiano Df(x).
3. Eficiente: Cálculo rápido de f⁻¹ y detDf(x).

Como en todo problema de optimización, debemos de fijar la función de coste que buscamos maximizar, en este caso esta función es:

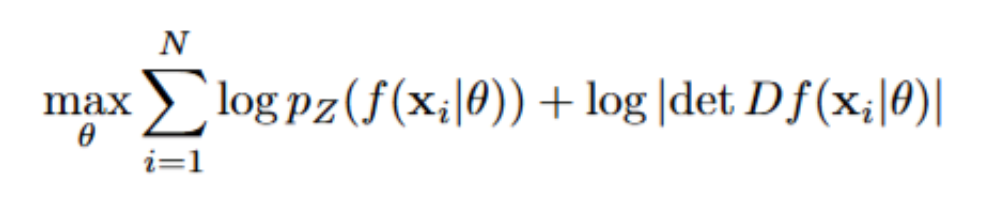
Para construir esta función f (normalmente a la que se refiere como el Flow), lo que se suele hacer es escribirla como una composición de funciones:  f=f_K​∘⋯∘f₁​, donde cada f_k​ es invertible, diferenciable y eficiente, lo que nos asegura que la composición: f también lo sea, además de ello, el jacobiano total es el producto de los jacobianos individuales:

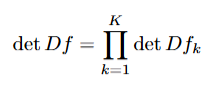
Lo que permite el calculo eficiente de la función que buscamos maximizar

Sobre estas funciones diferentes tipos que podemos implementar, las mas comunes son:

1. Lineales/Afines:  f(x)=Ax+b
   • Son funciones fáciles, intuitivas y sencillas de implementar, pero solo pueden ajustar la media y la varianza de la función, por lo que no incluyen gran complejidad.
2. Autoregresivos: f(x_i​)=μ_i​(x_1:i−1​)+σ_i​(x_1:i−1​)⋅x_i
   • Están descritas de una manera en la que el valor del siguiente punto transformado en el vector depende de los anteriores, esto permite introducir secuencialidad y crear modelos mas complejos, a cambio de un coste computacional mayor.
3. Coupling Flows: f(x)=(x^A​,f^​(x^B​∣θ(x^A​))).
   • Consiste primero en dividir el set de datos x en  dos subsets x^A​ y x^B, Solamente se transforman los datos de x^B​ , pero esto se hace de tal manera que los parámetros de estas transformaciones dependan de x^A, esto lleva a que se incluya mas complejidad y se establezcan relaciones entre los datos.

Para la generación de datos  el método es simple:

1. Se obtiene un elemento z cualquiera del espacio Z, distribuciones de ruido gaussiano
2. Se calculala función  f^^-1(z), que es la conjugación de las inversas: f=f^^-1₁​∘⋯∘f^{^-1}_K
3. Se aplica f^^-1(z) y se obtiene un dato x´ el cual se asemejará a los datos usados para entrenar el modelo, ya que proviene de la misma distribución

De esta manera podemos generar grandes cantidades de datos sintéticos a raíz de un buen modelo de Normalizing Flows. Para aquellos atento al blog es posible que este tipo de modelos os hayan recordado a los Modelos de Difusión. En verdad son dos modelos similares, de generación de datos desde el ruido, sin embargo tienen una diferencia principal: los Normalizing Flows permiten calcular la función de densidad explícitamente, los modelos de Difusión lo hacen implícitamente, y no se preocupan por calcular esta función, si no de usarla para obtener los datos que se buscan.

Como veis no paramos de trabajar y de mostrar nuevos modelos útiles para la generación de datos, continuad atentos al blog!