Los modelos de AutoRegressive Integrated Moving Average (ARIMA) o Seasonal ARIMA (SARIMA) son modelos que se usan exclusivamente con datos que vienen en forma de series temporales. Están formados por diferentes componentes que se unen para la predicción de los próximos datos en la serie temporal (denominado normalmente forecasting), para entender estos modelos describiremos ahora cada uno de sus componentes:
Modelos Autorregresivos (AR):
Un modelo autorregresivos utiliza una serie de puntos anteriores en la serie temporal para predecir el siguiente punto. Parte de la idea de que la tendencia que se ha establecido durante los puntos anteriores continuará en los siguientes.
En el modelo de ARIMA, AR hace referencia a esto y se representa como AR(p), donde esta p hace referencia al número de puntos anteriores que queremos seleccionar para predecir el siguiente.
Moving Average (MA)
Un modelo de Moving Average utiliza los errores en las predicciones pasadas para predecir el siguiente punto en la serie temporal. Parte de la idea de aprender de los errores de las predicciones pasadas para que no se repitan.
En el modelo de ARIMA, MA hace referencia a esto y se representa como MA(q), donde esta q hace referencia al número de errores anteriores que queremos seleccionar para predecir el siguiente punto.
Integrated (I)
Los modelos autorregresivos y de Moving Average son un tipo de modelos que asumen estacionariedad.
En las series temporales, la estacionariedad significa que las propiedades estadísticas (como la media, varianza y autocorrelación) son constantes en el tiempo
En particular, si una serie es estacionaria, entonces la distribución conjunta de los datos depende solo de las diferencias temporales, y no del momento específico en el que se observan.
Esto se puede observar en la siguiente imagen:
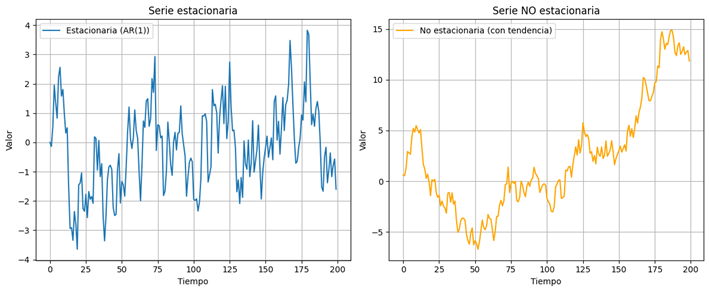
Los modelos autoregresivos y los de moving average precisan que el tipo de dato que tengamos provenga de una serie temporal estacionaria, si no lo son tendremos que transformarlos usando la diferenciación. Una diferenciación de grado 1 elimina las tendencias lineales en los datos, de grado dos las tendencias cuadráticas y así sucesivamente.
En el modelo de ARIMA, la I hace referencia a esto y se representa como I(d), donde esta d hace referencia al número de grados de diferenciación.
ARIMA:
De esta manera un modelo de ARIMA (p,d,q) primero diferencia los datos para convertirlos a estacionarios (I), utiliza anteriores puntos para predecir el siguiente (AR) y los errores pasados para una mejor predicción de este punto (MA).
SARIMA:
En el modelo de SARIMA, las siglas de ARIMA son las mismas que las descritas anteriormente, pero se incluye un nuevo elemento que es el de la Seasonality o Estacionalidad (que no estacionaria).
Esto se añade cuando los datos cuando hay un patrón que se repite en los datos temporalmente, por ejemplo: un patrón que se puede repetir a diario ( como por ejemplo más uso de red por la mañana que por la tarde debido a los trabajos), semanalmente (como el uso de red siendo menor los fin de semana porque la gente no trabaja) o anualmente (como el uso de red siendo más bajo en agosto o diciembre, cuando la gente está de vacaciones). Los datos entonces pueden tener diferentes estacionalidades que vienen representadas en el modelo de SARIMA.
De esta manera un modelo de SARIMA(p, d, q)(P, D, Q)s donde:
- (p, d, q) son los parámetros de ARIMA como hemos explicado anteriormente
- (P, D, Q) so los parámetros de ARIMA para la estacionalidad
- s implica la longitud del ciclo de «estación», por ejemplo si tenemos un dato cada hora, y tenemos una estacionalidad diaria s tomaría un valor de s = 24, si añadimos otra estacionalidad, tendríamos una segunda s2, cuyo valor seria s2=(24×7)=168
ARIMA y SARIMA son modelos muy usados para la predicción de datos futuros, para la generación de datos sintéticos, podemos usar una pequeña parte de una secuencia real y generar el resto usando estos modelos.
¡Para continuar aprendiendo sobre los trabajos que hacemos con estos modelos para la generación de datos, estad atentos al blog!
