La generación de datos sintéticos es una herramienta muy útil, como ya se ha comentado en entradas anteriores del blog. Sin embargo, tenemos que analizar que, en efecto estos datos generados sean representaciones fiables de las características de las series temporales originales, además de introducir suficiente variabilidad a estas. A continuación se muestra técnicas que se pueden utilizar para la evaluación de estas.

Visualización Comparativa de Series Temporales

Visualizar las series temporales sintéticas y compararlas con las reales visualmente nos puede dar una primera idea de las diferencias entre ambas. Por lo tanto, la primera técnica que vamos a aplicar es la comparación de las seires temporales superpuestas.

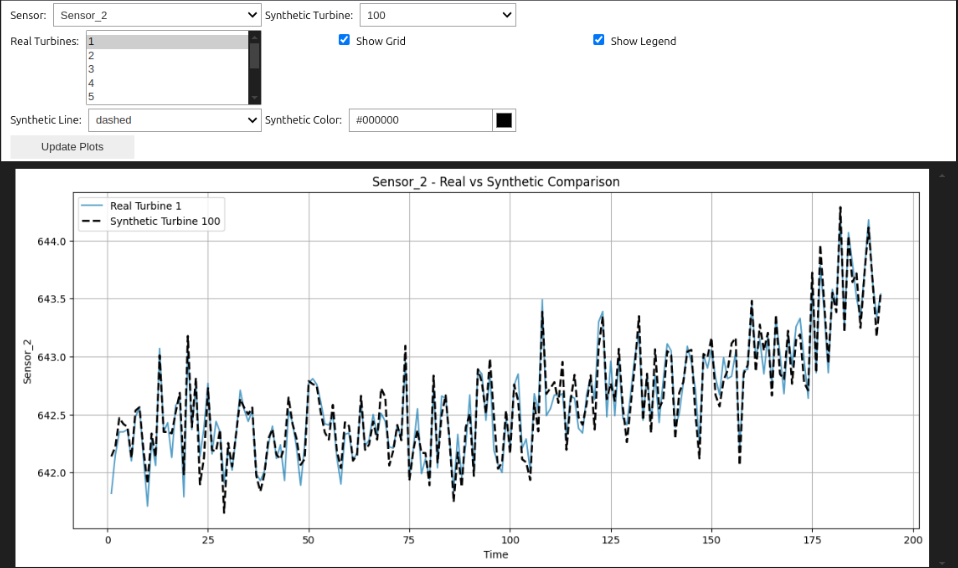
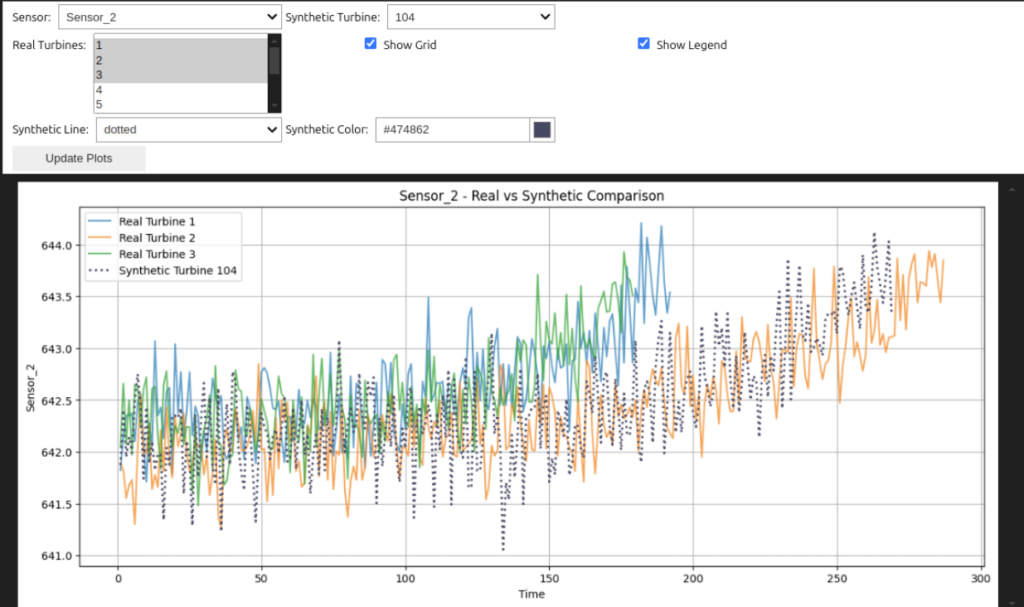
Prueba de Kolmogorov-Smirnov (K-S)

La prueba de Kolmogorov-Smirnov es una herramienta estadística que evalúa si dos muestras provienen de la misma distribución. Se basa en la comparación de las funciones de distribución acumulada (CDF) de ambas muestras y calcula la máxima diferencia entre ellas. Si esta diferencia es significativa, se rechaza la hipótesis nula de que ambas muestras comparten la misma distribución. Esta prueba es especialmente útil para detectar diferencias en la forma, posición y dispersión de las distribuciones.​OpenTURNSNoesis

Gráfico Q-Q (Quantile-Quantile Plot)

El gráfico Q-Q es una representación visual que compara los cuantiles de dos distribuciones. Si ambas distribuciones son similares, los puntos del gráfico se alinearán aproximadamente sobre la línea diagonal. Desviaciones de esta línea indican diferencias entre las distribuciones, como asimetrías o diferencias en la curtosis. Este método es particularmente útil para detectar discrepancias en los extremos de las distribuciones.​

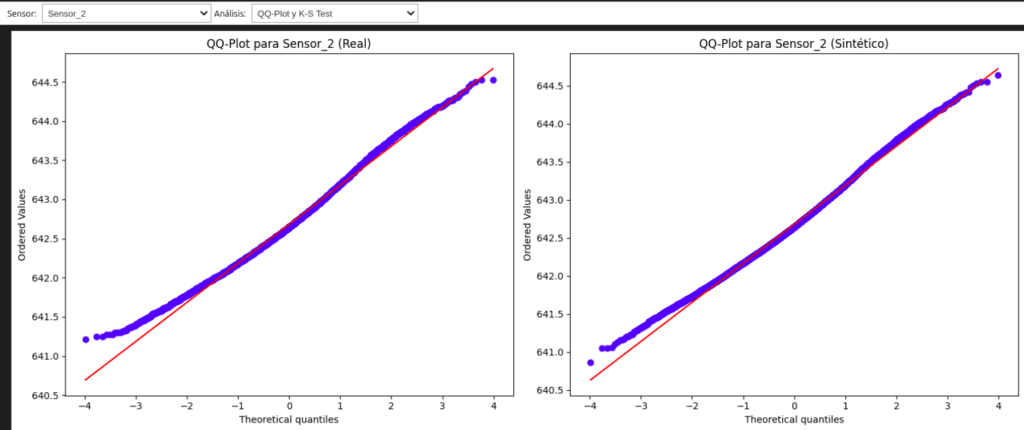
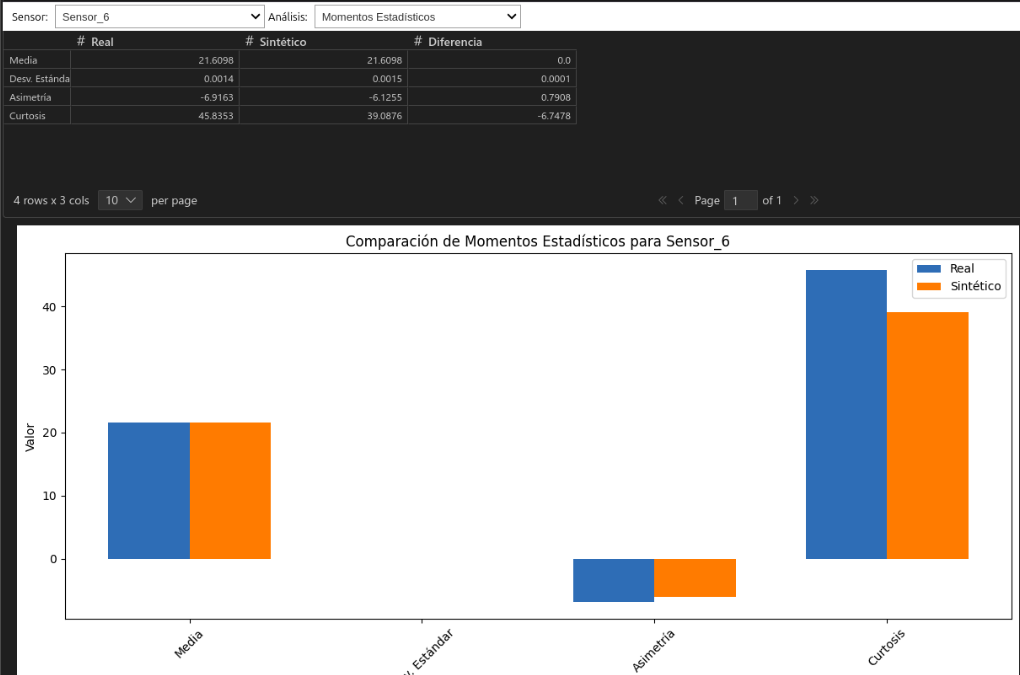
Análisis de Momentos Estadísticos

Los momentos estadísticos son medidas que describen características fundamentales de una distribución:​

• Media: Indica el valor promedio de la serie y proporciona información sobre la ubicación central de los datos.​
• Varianza: Mide la dispersión de los datos alrededor de la media, reflejando la variabilidad de la serie.​
• Asimetría (Skewness): Evalúa la simetría de la distribución. Una asimetría positiva indica una cola más larga a la derecha, mientras que una negativa señala una cola más larga a la izquierda.​
• Curtosis: Mide la «agudeza» de la distribución. Una curtosis alta indica una distribución con colas más pesadas, mientras que una baja sugiere colas más ligeras.​

Comparar estos momentos entre series reales y sintéticas permite evaluar si las propiedades fundamentales de las distribuciones coinciden, proporcionando una validación cuantitativa de la similitud entre ambas.​

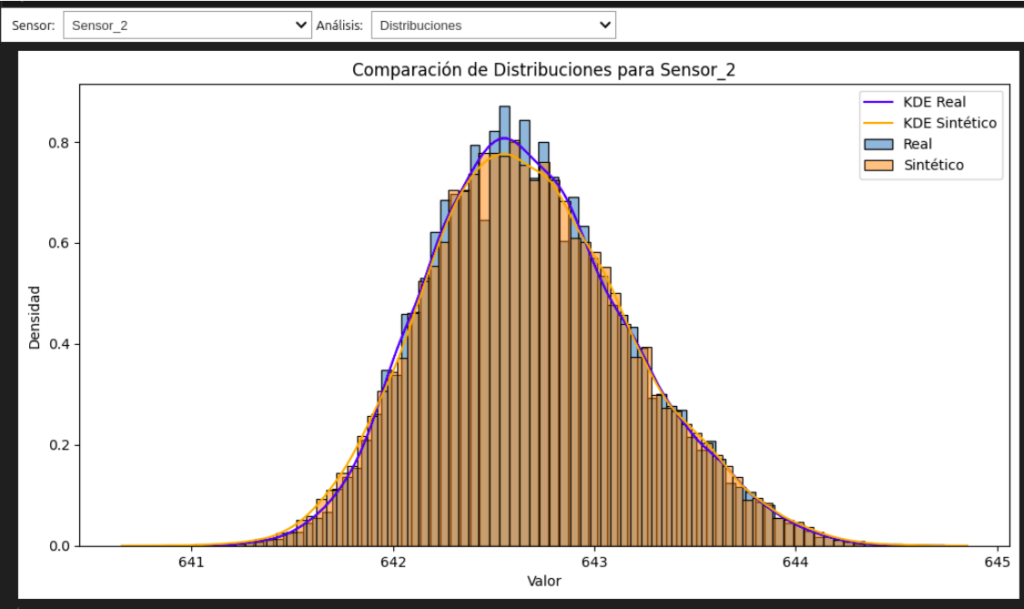
Conclusiones

En esta entrada hemos visto por encima cómo podemos hacernos una idea de la calidad de nuestros datos sintéticos. La visualización de estas evaluciones es esencial para determinar la calidad de los datos, aunque harían falta análisis más avanzados y específicos del caso de uso para comprobar si estos datos aportan suficiente variabilidad o son lo suficientemente fiables como para mejorar el rendimiento del modelo por el cual son utilizados.