Para esta entrada del blog os pido que saquéis vuestro lado más matemático, ya que para entrar en detalle sobre estas estructuras es necesario explicar las matemáticas que hay detrás.

La base de las Boltzmann Machines, son las Hopfield Networks, estas son unas estructuras determinísticas de caracterización de datos. Son simples y están formadas por una estructura de neuronas conectadas entre ellas que toman solo valores binarios (-1 o 1).  Por lo que no son suficientemente complejas para poder llevar a cabo problemas con los que nos encontramos hoy en día

En 1985, Geoffrey Hinton y Terrence Sejnowski, publican un artículo en el que introducen lo que denominan las Boltzmann Machines [1], a este enfoque de las Hopfield Networks se les introduce un elemento estocástico en forma de probabilidades, lo que hace al algoritmo mas complejo y permite representar problemas más complejos también.

La estructura de las Boltzmann Machines es de :

• Neuronas: Las cuales describimos como xi, y que tienen valores binarios (bien 1 o -1).
• Conexiones: Entre las neuronas, que describimos como w_{ij} y que tienen varias características:

1. Todas las neuronas estan conectadas entre ellas (Fully connected Layer)

2. Los pesos son simetricos (w_{ij} = w_{ji})

Como la mayoría de algoritmos, las Boltzmann Machines son un problema de optimización en el cual tenemos que reducir una función de coste.

En este caso, la función de coste es:

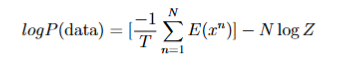
Donde:

• T: hace referencia a la temperatura, pero realmente es una constante que podemos fijar
• E(x^n): es la energía del dato, definida como:

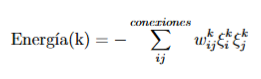
De tal manera que la energía de un dato k, es igual a la suma del producto de los pesos por los estados de las neuronas de todas las conexiones en la red de neuronas.

• N: Es el número total de neuronas
• Z: Es un factor de normalización calculado a raíz de todas las probabilidades.

Aunque haya muchas matemáticas en el modelo, la manera en la que se calcula acaba siendo simple:

Primero tenemos que calcular los pesos, para ello iteramos utilizando la Contrastive Hebbian Rule, que combina dos elementos:

1. Hebbiano: Refuerza conexiones entre neuronas que se activan juntas en los datos reales.
2. Anti-Hebbiano: Reduce el ruido ajustando conexiones que aparecen en datos aleatorios.

El aprendizaje se realiza iterativamente:

1. Se inicializan los estados y pesos aleatoriamente.
2. Se generan datos artificiales con esas condiciones.
3. Se calcula la media de activaciones en datos reales y sintéticos.
4. Se actualizan los pesos y se repite el proceso.

Una vez establecida la función, podemos clasificar un nuevo punto iterando de nuevo:

1. Se inicializan los estados aleatoriamente.
2. Se elige una neurona al azar para comenzar
3. Se calcula la energía de las conexiones de esas neuronas con el resto
4. Se utiliza la función sigmoide para convertir ese resultado en una probabilidad.
5. Se elige que la neurona tenga valor +1 o -1 dependiendo de esta probabilidad.
6. Se elige otra neurona y se repiten los pasos 2-5 hasta llegar a un mínimo local.

El número total de neuronas será el número de grados de libertad que tengan los datos. A estas neuronas se les sumarán unas neuronas ocultas, las cuales se entrenarán infiriendo información de los datos en lugar de obteniéndolos de una manera explícita.

Es gracias al aporte estocástico y a estas neuronas ocultas que se pueden llegar a obtener resultados complejos con estas estructuras, sin embargo,  la mayor limitación de estas estructuras es calcular todas las relaciones entre neuronas ya que esto puede llevar mucho tiempo. Por lo que en la práctica se suelen usar las Resticted Boltzman Macines, que solo permiten conexiones entre neuronas visibles y ocultas, y no entre ellas mismas.

Aunque esta técnica tiene aplicaciones para la generación de datos sintéticos como en [2], donde se usa para generar música Jazz, las principales aplicaciones de esta técnica son para comprobar que los datos sintéticos tienen valor por si solos [3]. Os seguiremos informando de técnicas interesantes en este ámbito. Atentos al blog!

REFERENCIAS:

[1] Hinton, G. E., & Sejnowski, T. J. (1986). Learning and relearning in Boltzmann machines. Parallel distributed processing: Explorations in the microstructure of cognition, 1(282-317), 2.

[2] Bickerman, G., Bosley, S., Swire, P., & Keller, R. M. (2010, January). Learning to Create Jazz Melodies Using Deep Belief Nets. In ICCC (pp. 228-237).

[3] Hess, M., Hackenberg, M., & Binder, H. (2020). Exploring generative deep learning for omics data using log-linear models. Bioinformatics, 36(20), 5045-5053.