Comenzamos este maravilloso mes de Abril con otro tipo de modelo estadístico generativo, en este caso los Kernel Density Functions. La motivacion de este tipo de algoritmos es ser capaces de describir la función de densidad de una población basándonos unicamente en una muestra limitada de esta. Es importante que entendamos a que nos referimos por Kernel, definimos Kernel como función de densidad de los datos.

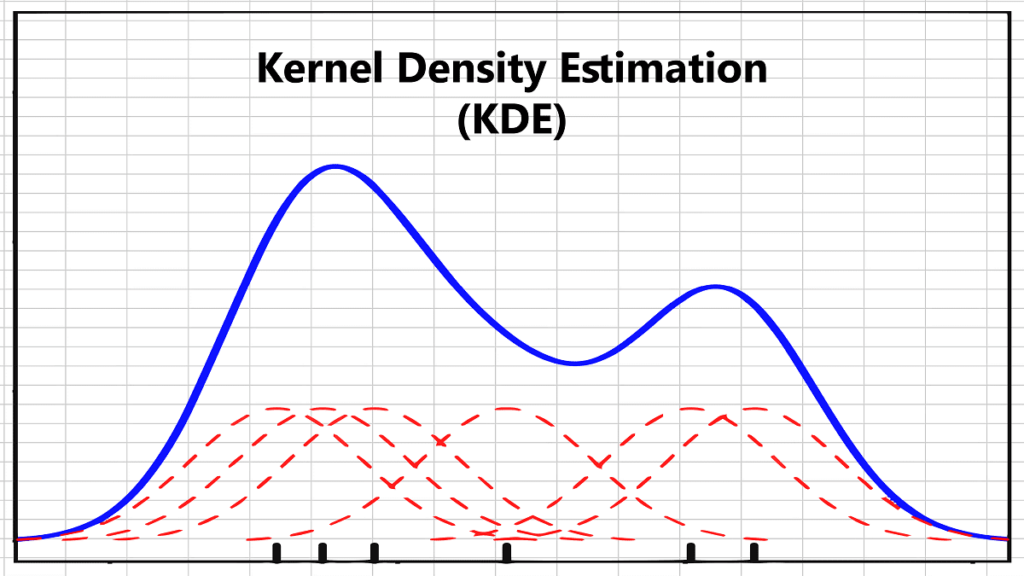
El principio en el que se basa esta técnica es que si tenemos un dato de un individuo x_i, este individuo nos está dando una idea de como es la densidad local del Kernel en ese punto, de manera que si hacemos esto,poniendo un kernel en cada uno de nuestros datos, la función de densidad total será la suma de estos kernels, normalizada para obtener una probabilidad entre 0 y 1.

Visualmente podemos entenderlo mirando la siguiente imagen [1], centrando un kernel en cada dato, la función de densidad total será la suma total normalizada de estos.

La función de distribución final se describe como:

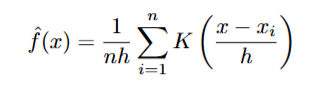
donde:
– n es el número de muestras.
– h es el ancho de banda.
– K(u) es la función de kernel.

El kernel mas utilizado es una distribución normal sobre el dato, pero hay otros casos:

Kernel Gaussiano: Simple, eficiente y suave

Kernel Uniforme: Es muy eficiente de calcular, pero no es suave y tiene picos abruptos, se usapara una estimación simple

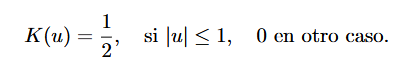
Kernel Epanechnikov: Se usa cuando los datos están más concentrados en un rango específico

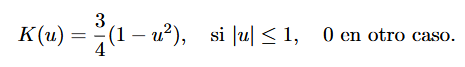
Kernel Coseno: usado cuando los datos tienen una estructura periódica

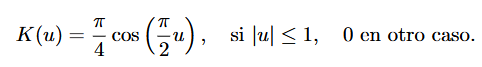
Algo importante en este lugar es elegir la anchura de los kernels que centramos en cada uno de los datos, lgunas manera de elegir esto es usando:

• Reglas fijadas: La mas usada es la de Silveman:

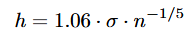
• Plug-in Selector: Usa estimaciones previas para elegir h de manera ´optima.

• Cross-validation: Minimiza el error de validaci´on cruzada para encontrar el mejor h.

• Inspección Visual: Se prueba con diferentes valores de h y se elige el más adecuado observandola suavidad de la distribución.

Si conseguimos adecuar la función de densidad a los datos, podemos usar esta función aproximada f^{^}(x) para generar datos sintéticos que provienen de la misma distribución que el original y por tanto se asemejarán mucho a los reales, además tendremos también una expresión explícita de la función de densidad de los datos. Los modelos Estadísticos Generativos son muy interesantes, y os iremos trayendo mas al blog.

REFERENCIAS

[1] https://numxl.com/blogs/kernel-density-estimation-kde-plot/