Uno de los mayores retos en el mantenimiento predictivo del sector aeroespacial es la falta de datos representativos, especialmente de fallos reales (como ya hemos visto en entradas anteriores). En motores de helicópteros o aeronaves, los sistemas de control y supervisión recogen miles de variables en tiempo real, pero casi todos esos registros pertenecen a vuelos normales. Los fallos graves son raros, y cuando ocurren, apenas hay unos pocos ejemplos. Esta escasez de datos limita el desarrollo de modelos inteligentes capaces de detectar anomalías o anticipar averías.
Para abordar este problema, en nuestro estudio decidimos explorar una idea sencilla pero poderosa: crear más datos buenos, es decir, generar artificialmente nuevos ejemplos de funcionamiento normal que sean estadísticamente indistinguibles de los reales. Si el modelo aprende mejor qué es un comportamiento “normal”, podrá detectar con más precisión cuándo algo se sale de ese patrón.
¿Qué es un Modelo de Mezclas Gaussianas?
Un GMM (Gaussian Mixture Model) es una técnica estadística clásica que permite representar distribuciones de datos complejas mediante la combinación de varias distribuciones normales (o “Gaussianas”).
Imaginemos que los datos de un motor no siguen un único patrón de comportamiento, sino varios: distintos regímenes de vuelo, cambios de temperatura, variaciones de potencia, etc. Cada uno de esos “modos” de operación puede verse como una nube de puntos en un espacio multidimensional (uno por cada sensor).
El GMM lo que hace es ajustar una Gaussiana a cada una de esas nubes y luego las combina, de forma ponderada, para formar un modelo global que describe cómo se distribuyen los datos normales en su conjunto. De este modo, se obtiene una representación flexible y realista de los diferentes estados del motor.
Una vez entrenado, el modelo permite muestrear nuevos puntos: generar observaciones artificiales que siguen las mismas relaciones estadísticas entre sensores que los datos reales. Esos nuevos puntos son los llamados datos sintéticos.
Entrenando el modelo con datos reales
En nuestro caso, el modelo GMM se entrenó únicamente con datos de funcionamiento normal del motor, extraídos de un conjunto de medidas de telemetría de siete sensores distintos (temperatura del aire exterior, potencia, velocidad del compresor, par de salida, etc.).
Antes del entrenamiento, todos los datos se normalizaron entre 0 y 1 para que las variables fueran comparables y ninguna dominara sobre las demás. Luego, el algoritmo estimó automáticamente cuántas “subpoblaciones” Gaussianas eran necesarias para describir el comportamiento del motor. Para ello se utilizó el criterio BIC (Bayesian Information Criterion), una métrica que equilibra precisión y complejidad. El mejor resultado se obtuvo con 12 componentes, lo que sugiere que el motor tiene múltiples regímenes de operación bien diferenciados.
Cada una de esas 12 “microdistribuciones” modela una parte del espacio de operación del motor: por ejemplo, las condiciones típicas de crucero o las variaciones de temperatura bajo distintas cargas.
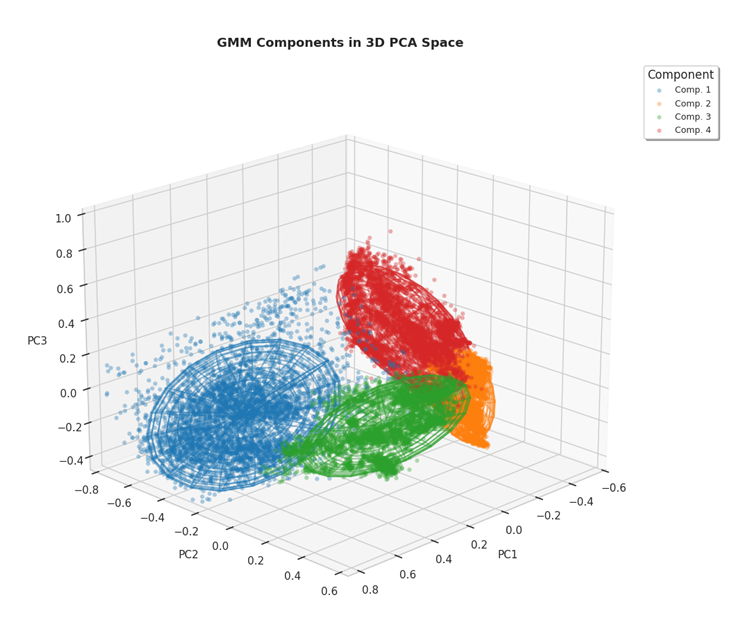
Filtrado y validación de los datos generados
El proceso no termina al generar puntos nuevos. Uno de los riesgos al crear datos sintéticos es salirse del dominio físico realista, produciendo valores imposibles o poco probables.
Para evitarlo, aplicamos una cadena de filtros de validación que garantizan que los datos generados no se alejen demasiado de los observados en la realidad:
- Filtrado por distancia de Mahalanobis local: mide qué tan lejos está cada punto sintético respecto al centro de su componente GMM, considerando la correlación entre variables. Solo se aceptan aquellos dentro del 85 % más representativo de los datos reales.
- Filtrado por verosimilitud (log-likelihood): descarta los puntos que, aunque estén dentro de la nube, tienen una probabilidad demasiado baja según el modelo.
- Filtrado global de respaldo: un filtro más general que asegura que, en conjunto, todos los puntos se mantengan dentro del rango típico del sistema.
- Control físico: cualquier valor que exceda los rangos reales de los sensores es eliminado.
- Filtro de diversidad δ: elimina duplicados o puntos demasiado cercanos entre sí para mantener la variedad de ejemplos.
Con todo este proceso, los datos sintéticos finales son realistas, variados y físicamente coherentes con el sistema real. En el estudio también se aplicaron pruebas estadísticas (como el test de Kolmogorov–Smirnov) para confirmar que las distribuciones reales y las generadas coincidían con un alto grado de fidelidad.
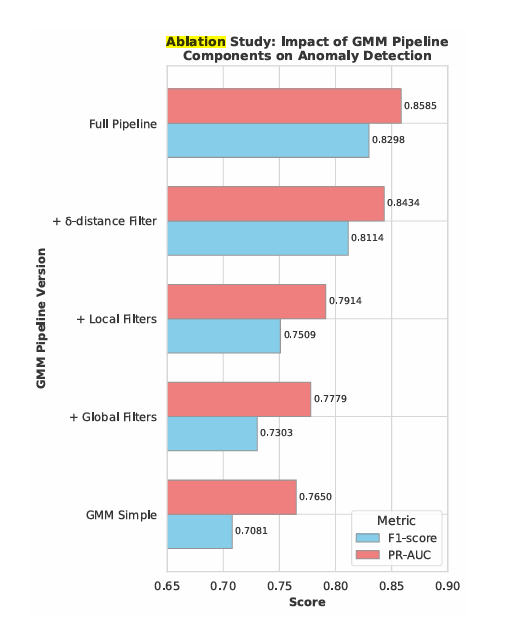
Integración con el modelo de detección de anomalías
Una vez generados, estos datos sintéticos se combinaron con los reales para entrenar un autoencoder, un modelo no supervisado que aprende cómo debe comportarse el sistema en condiciones normales.
El autoencoder intenta reconstruir sus propias entradas; cuando recibe un dato fuera de lo normal (por ejemplo, un fallo), su error de reconstrucción aumenta notablemente. Esa diferencia se utiliza como indicador de anomalía, medido mediante la distancia de Mahalanobis entre el error y el patrón típico aprendido durante el entrenamiento.
Resultados: una mejora clara
Los experimentos mostraron que los datos generados con GMM mejoraron significativamente el rendimiento del autoencoder, especialmente cuando el conjunto de datos reales era pequeño.
Por ejemplo, cuando solo se disponía del 10 % de los datos reales, el modelo original alcanzaba un F1-score de 0.68. Tras añadir datos sintéticos generados con el GMM, el F1-score subió a 0.83, superando incluso al modelo entrenado con el 25 % de los datos reales.
Esto demuestra que, con un buen proceso de generación, los datos sintéticos pueden compensar la falta de información real sin perder calidad estadística.
| Escenario | Precisión | Exhaustividad (Recall) | F1-score | Exactitud (Accuracy) |
|---|---|---|---|---|
| A1 (25% Real) | 0.7731 | 0.6799 | 0.7235 | 0.7927 |
| A2.1 (25% + GMM×1) | 0.8248 | 0.8206 | 0.8227 | 0.8589 |
| A2.2 (25% + GMM×2) | 0.8346 | 0.8534 | 0.8439 | 0.8740 |
| A4 (10% Real) | 0.7585 | 0.6155 | 0.6796 | 0.7684 |
| A5.1 (10% + GMM×2) | 0.8082 | 0.8008 | 0.8045 | 0.8447 |
| A5.2 (10% + GMM×3) | 0.8285 | 0.8312 | 0.8298 | 0.8640 |
Un paso hacia el mantenimiento predictivo real
En el ámbito aeroespacial, donde obtener datos de fallos es extremadamente difícil (y peligroso), los GMMss ofrecen una forma segura y controlada de ampliar la información disponible.
Esto no solo permite mejorar la precisión de los modelos de detección de anomalías, sino también acelerar el desarrollo de sistemas predictivos sin comprometer la seguridad. Además, los GMM son modelos interpretables, reproducibles y eficientes computacionalmente, lo que los convierte en una herramienta idónea para entornos industriales.
En definitiva, la generación de datos sintéticos mediante Modelos de Mezclas Gaussianas representa una vía sólida para entrenar sistemas de mantenimiento predictivo más inteligentes, capaces de detectar desviaciones sutiles antes de que se conviertan en fallos críticos.
Una forma de seguir aumentando la seguridad de la aviación, sin necesidad de esperar a que los errores ocurran.
