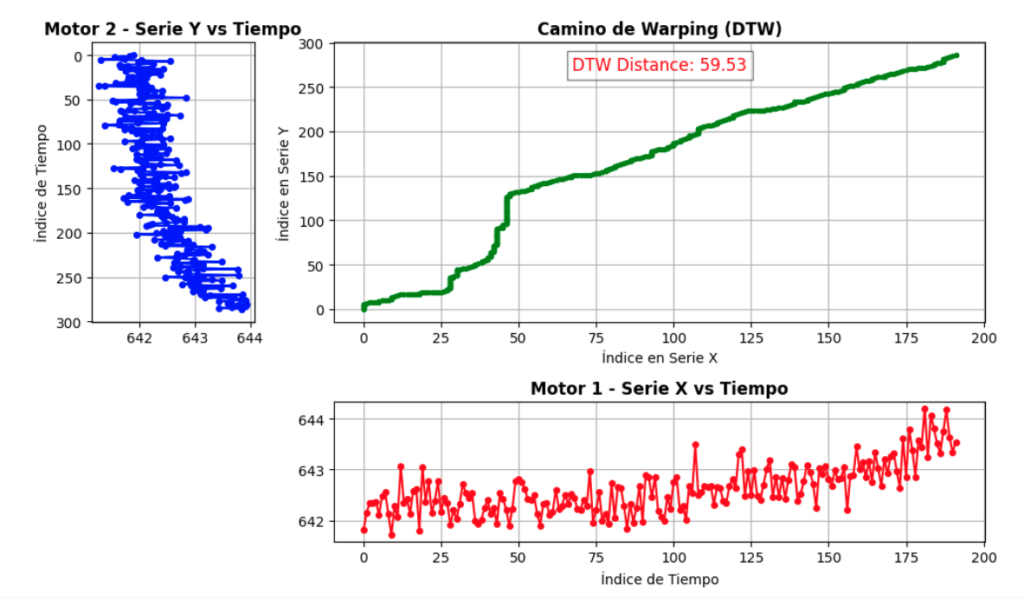
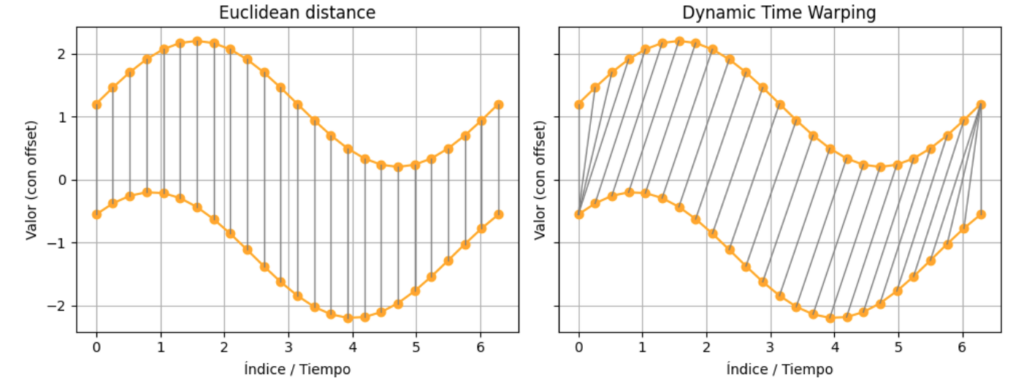
A la hora de comparar dos series temporales, la distancia euclídea puede fallar si una de ellas está desfasada o si se mueven a diferentes velocidades. Para resolver este problema se inventó Dynamic Time Warping (DTW), que básicamente busca la mejor forma de “emparejar” los puntos de ambas series, de modo que se minimice la diferencia total entre ellas.
Imagina que tienes dos series que son muy similares, pero una está desplazada hacia la derecha. Con la distancia euclídea, compararías los puntos que caen en el mismo instante, lo que podría dar una diferencia muy alta. En cambio, DTW se encarga de encontrar qué punto de una serie corresponde mejor a cada punto de la otra, sin importar su posición en el tiempo. Así, en lugar de medir la diferencia entre instantes, se mide entre las características de la señal.
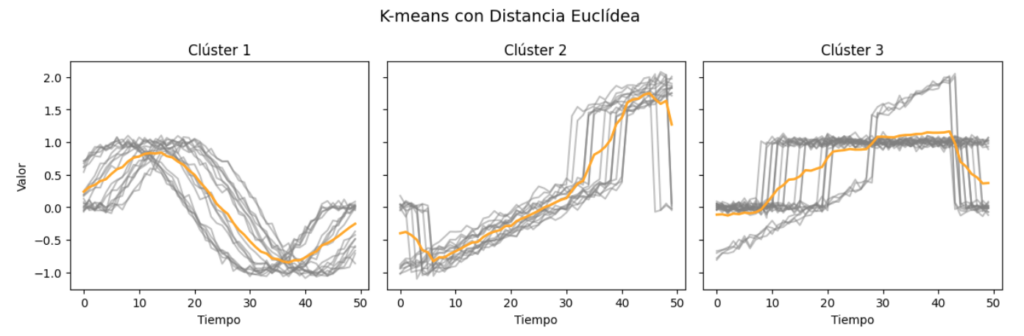
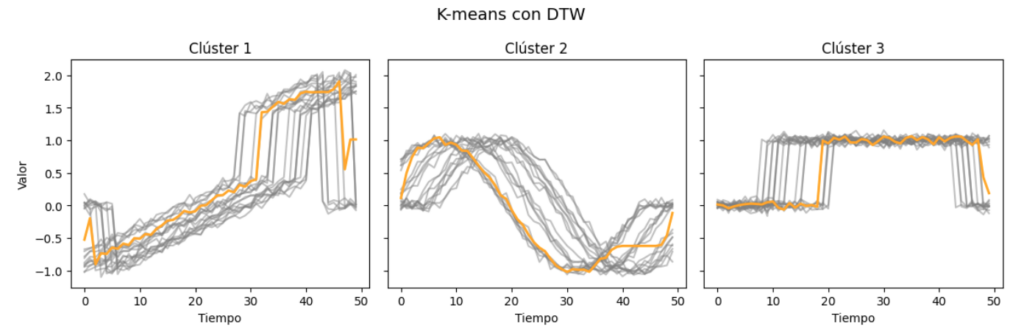
Esta capacidad es útil por ejemplo cuando se hace clustering (agrupación) de series temporales. Gracias a DTW, podemos agrupar señales que tienen la misma forma o patrón, aunque estén desplazadas o tengan variaciones en la velocidad. Por ejemplo, en un experimento se compararon tres tipos de señales. Cuando se utilizó la distancia euclídea, en uno de los grupos el centroide (la “media” de las señales) no representaba bien a sus miembros, pero con DTW, el centroide resultó mucho más fiel a la forma común de ese grupo.
¿Cómo funciona DTW?
En lugar de probar todas las posibles formas de alinear las dos series (lo cual sería inviable porque hay demasiadas), DTW utiliza programación dinámica. La idea es construir una matriz de costos acumulados donde cada celda representa el “costo” mínimo necesario para alinear la parte inicial de la primera serie hasta ese punto con la parte inicial de la segunda serie.
- Inicialización:
Se crea una matriz RRR del mismo tamaño que las dos series. La primera celda R[0,0] se rellena con la diferencia (por ejemplo, el cuadrado de la diferencia) entre el primer elemento de ambas series. - Relleno de la matriz:
Para cada celda R[i,j], se calcula el costo de alinear el elemento x[i] con x′[j] y se suma al mínimo de los costos de las celdas vecinas (la de arriba, la de la izquierda o la diagonal superior izquierda). Esta operación se repite para llenar toda la matriz. - Resultado:
Al final, la última celda R[n−1,m−1] contiene el costo acumulado mínimo para alinear las series completas. Tomando, por ejemplo, la raíz cuadrada de ese valor (si usamos diferencias al cuadrado), obtenemos la distancia DTW.
Pseudocódigo
Aquí te dejo un pseudocódigo simplificado para que te hagas una idea de cómo se implementa DTW:
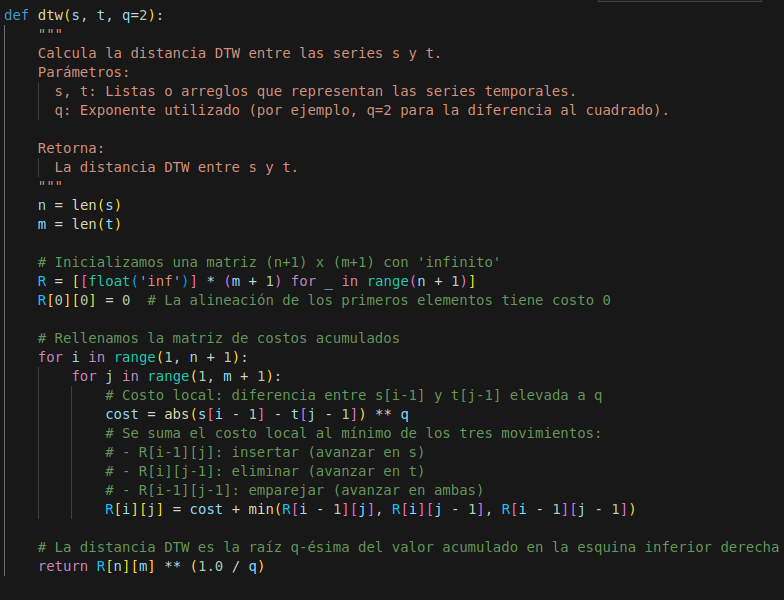
En pocas palabras, DTW te ayuda a encontrar la mejor forma de alinear dos series temporales, considerando que pueden estar desfasadas o tener velocidades diferentes, y así obtener una medida de similitud que refleja realmente la forma de las señales, y no solo la coincidencia en el tiempo.
Esta técnica es muy útil en clustering y otros análisis de series temporales, ya que permite agrupar señales que comparten características importantes, aunque no estén perfectamente sincronizadas.